The Book and Box of Fact Strategies Digital Sample- Addition

The make-ten strategy includes facts that have one addend close to 10. In these instances, 10 can be used as a reference point to help students figure out totals when one part involves 9, 8, or 7. For example, the total of 9+6 is the same as the total of 10+5. 

 

 

Make-Ten Facts 

 

There are 33 make-ten facts which includes the turnaround. Students will learn and extend these facts as they complete the activities on page 70-79. 

Did you know?​

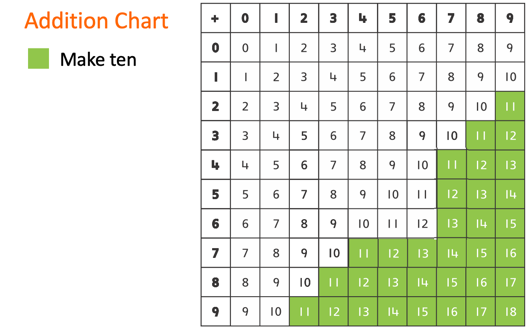
Make-ten strategy is also known as bridge to 10, bridge the decades, bridging across tens, bridging through 10, making 10, make to 10, and use 10. 

Total Ten (Addition Making Ten)

 

Focus

Reinforcing combinations that add to ten

Aim

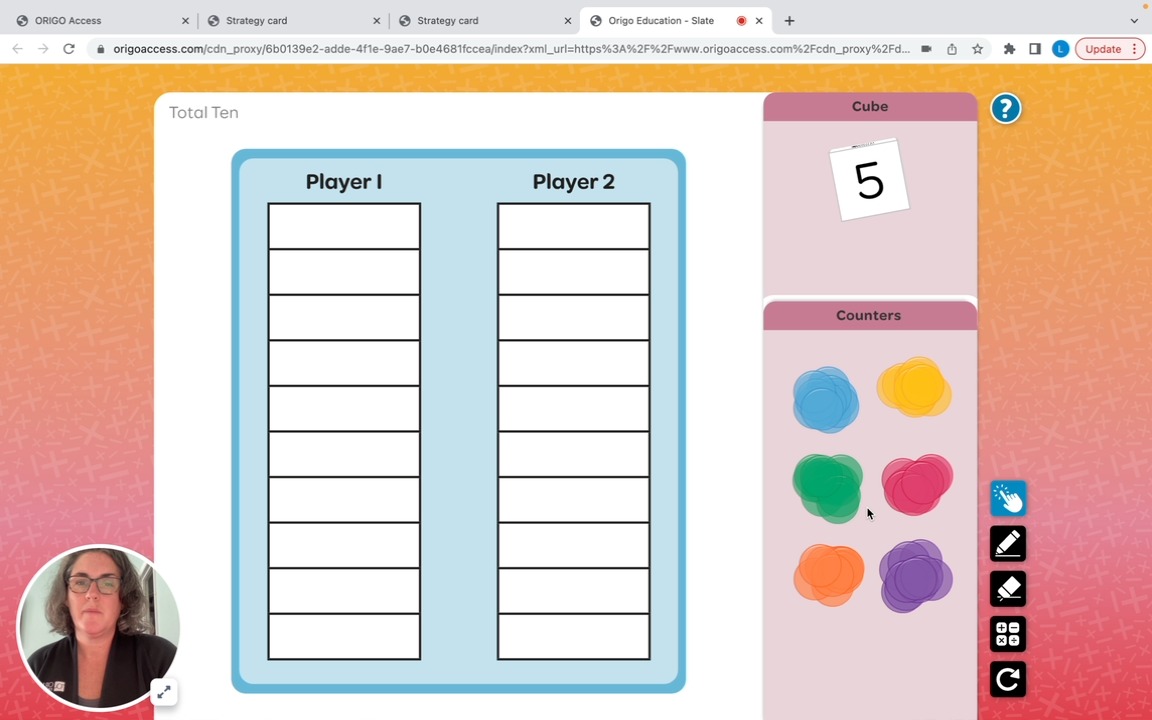
The first Player to fill their track with counters wins.

How to Play

1. Select the cube to make it roll and say the number.

2. Click and Drag counters on the track to represent the number rolled. Use different colored counters to show the number for each turn. If the number rolled does not fit on the track, the player misses a turn.

3. Play continues in turns until one player fills their track with counters.

Restart the Game

Watch how to play the game below!

 

Project the make-ten strategy card for 9+5, or demonstrate with card from Box. Ask, "What numbers do you see without counting? (9 and 5) What addition fact can we write about these numbers?" When suggested, write the equation 9+5=__ on the board. Say, "Turn to the student beside you and talk about how you could figure out the total." After a few minutes, invite pairs to share their thinking. Then ask, "What number do we add to nine to make ten?" 

Close the top flap of the card, as shown. Ask, "What numbers so you see now? What addition fact can we write to match?" When suggested, write the equation 10+4=__ on the board. Ask, "How else can we add 9 plus 5? which equation is easier to calculate?" Students should identify that, "Nine plus five is the same total as ten plus four." Repeat the discussion with the make-ten strategy card for 8+4.

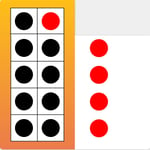
Watch the example below!

Check-In

• Can the student represent make-ten addition facts with concrete resources and pictures?
• Can the student decompose the lesser addend to make ten?

 

Reinforce Game Board

Organize students into groups of three. Distribute the number tracks , the double ten-frames, connecting cubes, and counters. Write 5+9=__ on the board. Ask the students in each group to use each resource to model the make-ten addition strategy. Then have them write the equation to show how they added. Observe students and ask questions such as, "Is it easier to start with 9 and add 5 or start with 5 and add 9? Why? Why did you jump to 10 first? How does that make the addition easier?" Repeat for 8+3, then 9+4.

 

Organize students into pairs. Distribute the double ten-frames and counters. Say, "Place 19 counters on the ten-frames and place 5 counters of a different color beside the ten-frames. How would you use the ten-frames to figure our 19+5?" Invite responses and highlight those that involve moving one counter to fill the ten-frames then adding 20 and 4. Project the number line and ask, "How can we show this strategy on the number line?" Invite a student to draw jumps on the number line to model the make-ten strategy. Then ask, "How could you use this thinking to figure out 29+5? What other numbers could you add using this strategy?"

 

Check In

• Does the student understand the make-ten strategy?
• Can the student apply the commutative property as needed to make the addition easier?
• Can the student represent make-ten addition facts with resources, with pictures, and in words?

Organize students into pairs and distribute empty game boards and counters. Write the numbers 11 to 18 on the board. Ask the students to write any of these numbers in any order to fill their game board. Explain that these numbers are the totals of make-ten addition facts and that some numbers will need to be used more than once to fill the grid. Students will need to think about which totals to repeat. For example, 12 is the total of 8+4, 9+3, and 7+5, so this is a strategic number to repeat. Mix the make-ten dominoes, then call out the expressions they represent, one at a time. The students place a counter on one matching total on their game board. The first student to fill their game board with counters calls out Bingo to win the game.

Check In

• Can the student accurately recall the make-ten addition facts?
• Does the student apply the commutative property to make the addition easier?

Organize students into pairs, distribute the double ten-frames and counters. Say, "Place 19 counters on the ten-frames and place 5 counters of a different color beside the ten-frames. How would you use the ten-frames to figure out 19+5=__?" Invite responses and highlight those that involve moving one counter to fill the ten-frames then adding 20 and 4, as shown below. Project the number line and ask, "How can we show this strategy on the number line?" Invite students to draw jumps on the number line to model the make-ten strategy. Then ask, "How could you use this thinking to figure out 29 + 5? What other numbers could you add using this strategy?"

Organize students into pairs. Distribute the number lines handouts. Project the equation 78+15=__ with the number line. Ask, "How can we use the make-ten strategy to add 78 and 15? Which number will we start with? Why? What jumps will we make? What equation will we write?" Encourage the students to discuss their ideas in their pairs. Then invite individuals to share and demonstrate their thinking, as shown below.

Some students may say, "I start with the greater number and make a jump to the nearest ten. 78 plus 2 is 80. There is 13 left to add, so 80 plus 13 is 93." Others may reason, "78 plus 10 is 88. 88 plus 2 is 90 and 90 plus 3 is 93." Record their equations on the board, for example, 78+15=80+13=93 or 78+10+2+3=93. Repeat with 87+24, then 99+16.

 

 

Check In

• Can the student extend the make-ten strategy to totals within 99?
• Can the student extend the make-ten strategy to totals within 120?
• Can the student solve multistep word problems that have one addend close to a multiple of 10?